Quick Sort

Quick sort

Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value.

Quicksort partitions an array and then calls itself recursively twice to sort the two resulting subarrays. This algorithm is quite efficient for large-sized data sets as its average and worst-case complexity are O(n²), respectively.

Steps:

Step 1: Divide

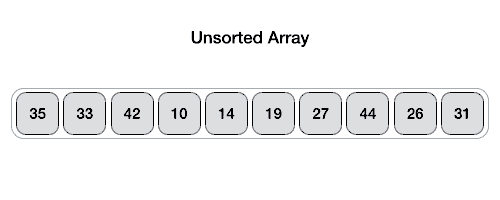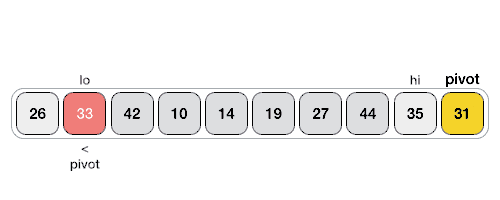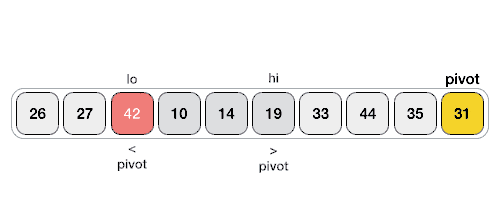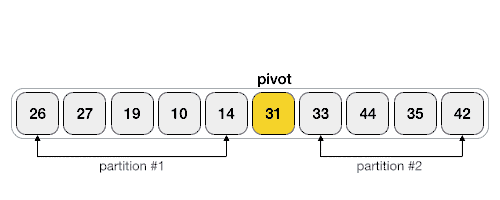
In this step at first, we choose a pivot. A pivot is any element from the array or subarray. In our discussion, we’ll always choose the rightmost element from a subarray as the pivot. After choosing the pivot we’ll rearrange the elements such a way that, all the elements that are less than or equal to the pivot are to its left and the elements that are greater than the pivot to its right. This procedure is called partitioning. After partitioning the pivot is in its final position.

How the partitioning works?

If the rightmost element is not chosen as the pivot, move it to the rightmost index. Now we start scanning the elements from the first index in left and from the next left element of pivot in right.

From left we look for the element that is greater than the pivot and from right we look for the element that is less than or equal to the pivot. When we find them, we swap the elements.

Now we keep continuing. If the index of the larger element than pivot ( say l ) is larger than the index of the smaller or equal element to pivot (say s) we stop. Now we swap the larger element ( at index l ) with the pivot.

Now we divide the array into two subarrays except the pivot. One subarray contains the left part of the pivot and another one contains the right part of the pivot. With this, the divide phase finishes for this array.

Step 2: Conquer

In this step, the subarrays will be recursively partitioned and sorted by fixing the position of the pivot of each subarray.

Step 3: Combining

This step doesn’t play a significant role in quicksort. At the end of conquering step the array is already sorted.